WACV2020에 발표된 논문이다. 적은 데이터셋과 scratch weight으로 학습 할 때 좋은 성능을 내는 방법에 관해 소개한다. (Arxiv)

Introduction

하드웨어의 발전으로 인해 매우 큰 dataset을 사용하고있다. 하지만 학습 데이터를 많이 모으기에는 한계가 존재하며 이를 위해 pre-trained 모델과 fine-tuning을 통하여 이를 극복할 수 있다. 하지만, pre-trained 모델을 사용한 transfer learning에는 문제 될만한 것이 두가지가 있다. 우선 의료 이미지 같이 target domain이 매우 special한 경우 기존(imageNet) 이미지와 큰 차이가 있으며, license의 문제 또한 존재한다.

이에 본 논문에는 softmax+cross-entropy에 대해 문제를 제기하면서, cosine loss function을 사용하여 small data without external information 문제를 해결하는 방법을 제시한다.

small dataset을 해결하기 위해 few-shot learning, metric learning, 그리고 meta-learning 기법이 존재한다. 하지만 이 기법들 모두 우선 large dataset을 사용해야 한다. 이 논문에서는 large dataset 없이 각 클래스당 20 ~ 100 개 미만의 학습 이미지로 이루어진 small dataset 만을 이용한다.

Cosine Loss

cosine similarity는 두 vector \(a, b \in R^{d}\)의 사이각을 이용한 유사도이다. 아래 식에서 \(<\cdot , \cdot>\)은 dot product를 뜻하며, \(\|\|_{p}\)는 \(L^{p}\) norm을 뜻한다.

\[\sigma_{cos}(a, b) = cos(a \angle b) = \frac{<a,b>}{\|a\|_{2} \cdot \|b\|_{2}}\]

\(x \in X\) 데이터와 \(y \in C\) label이 주어질 때, \(f_{\theta} \colon X \rightarrow R^{d}\) 를 통해 X는 d-dimensional feature space로 transform 된다. 그리고 \(\psi \colon R^{d} \rightarrow P\) 와 \(\varphi \colon C \rightarrow P\) 가 각각 feature와 classes를 prediction space P에 임베딩 시킨다.

\(\varphi\) 를 고정시키고, \(f_{theta}\) 의 파라미터를 학습 시켜서 이미지 feature와 각 class의 cosine simiairty를 극대화 시키는 것이 cosine loss function이며, 아래 식과 같다.

\[L_{cos}(x, y) = 1 - \sigma_{cos}(f_{\theta}(x), \varphi(y))\]

\(\psi = \frac{x}{\|x\|_{2}}\) 와 one-hot vector인 \(\varphi\) 를 사용하여 두 백터 \(f_{\theta}(x), \varphi(y)\) 를 unit hypersphere로 바꾸었다. 이로써 cosine similarity를 단순한 dot product로 구할 수 있게 되었다.

\[L_{cos}(x, y) = 1 - <\varphi(y), \psi(f_{\theta}(x))>\]

Comparison with Categorical Cross-Entropy and Mean Squared Error

cosine loss를 categorical cross-entropy loss 그리고 mean squared error(MSE)와 비교를 하였다. 가장 큰 차이점은 예측(predictions)과 ground-truth 와의 차이를 측정하는 방식에 있다.

categorical cross-entropy loss 그리고 mean squared error(MSE) 두 loss를 간단히 설명하면

• MSE는 feature space에 transform을 적용하지 않고, Euclidean prediction space를 이용한다. 위 unit hypersphere를 통한 \(L_{cos}\) 식을 풀어 쓰면 Euclidean distance와 매우 유사하다. (\(L^2\) Norm 값이 1로 고정 이기 때문에)
• Categorical cross-entropy는 Kullback-Leibler divergence를 이용하여 확률 분포(probability distribution) 공간의 차이를 측정하는 loss 이다. 이는 softmax 함수를 이용하여 prediction space로 transform 시킨다.

두 loss와 비교했을 때 cosine loss는 두 가지 특징이 있다.

• loss는 [0, 2] 경계로 되어있다. 반면에 다른 loss는 매우 큰 값을 가진다.
• feature vector의 direction 만을 고려하기 때문에, scaling에 invariant 하다.

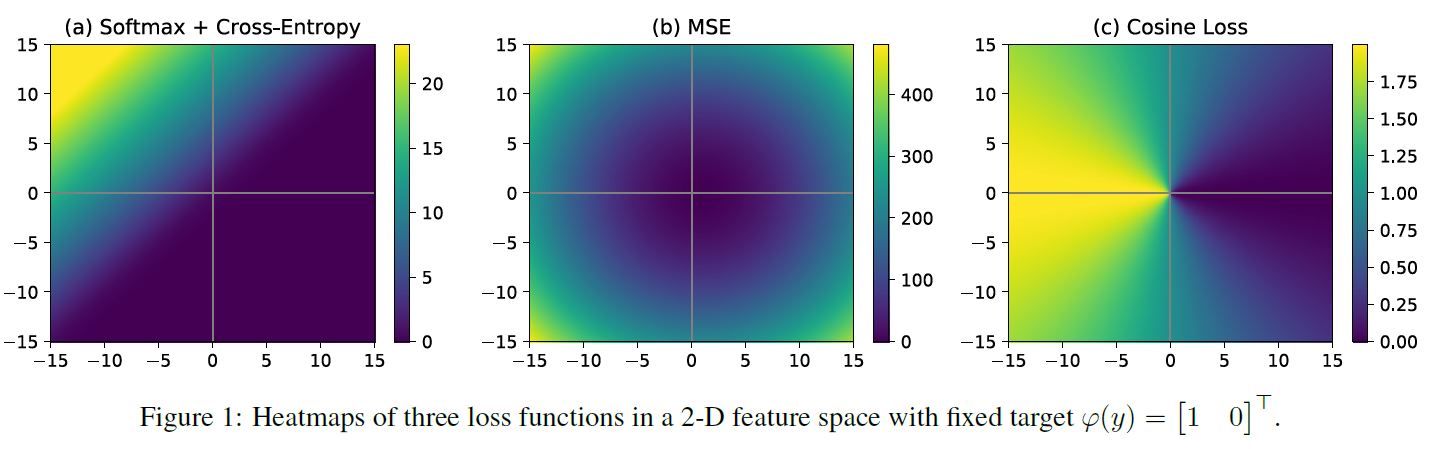
위 figure을 보면 cross entropy loss는 급강하 영역과 두 넓은 지역으로 이루어져있다. 밝은 부분과 어두운 부분은 일정하진 않지만 매우 차이가 적다. 따라서 초기화 및 learning rate 설정을 잘 해야할 것이다. 반면, figure 1.c cosine loss을 보면 색이 고르게 분포되어 있어서 더 robust 할 것이다.

또한 cross-entropy loss 는 true class의 값이 다른 class의 값 보다 헌저하게 커야만(혹은 infinity) optimum 한 값을 얻어진다. 따라서 적은 dataset을 이용하여 학습을 하면, overfitting이 일어날 수 있다. 보통 이 문제를 해결하기 위해 label smoothing 을 적용한다(ground-truth distribution 에 noise를 주어서 regularization). 간단하게 설명하자면 [1, 0, 0] 이라는 ground-truth 대신 [\(1-\varepsilon\), \(\frac{\varepsilon}{n-1}\), \(\frac{\varepsilon}{n-1}\)] 로 설정하는 것이다. 이때 \(\varepsilon\) 은 0.1 과 같은 작은 상수이다.

cosine loss는 \(L^{2}\) normalization이 regularizer 역할을 하여 \(\varepsilon\) 과 같은 hyper-parameter를 사용하지 않는다. 또한 높은 차원에서 문제가 되는 Euclidean distance를 사용하지 않고, 방향만을 고려하여 학습에 적용된다. 따라서 적은 dataset을 사용할 때, scaling에 invariance한 점이 좋은 regularizer로 작용된다.

Semantic Class Embeddings

위의 \(\varphi\) 같은 경우 class를 one-hot vector로 embedding 하였다. 하지만 one-hot vector에는 class 간의 semantic relationship이 고려 되어있지 않다. 이를 위해 WordNet과 같은 ontology를 이용하여 \(\varphi_{sem}\) class embedding 하였다 pdf. 이제 이미지의 smeantic consistency를 향상 시킬 수 있게 되었다.

하지만 분류 정확성을 위해 categorical cross-entropy와 함께 사용을 하였으며 그 식은 아래와 같다. \(g_{\theta}\) 는 softmax activation이 적용된 fully-connected layer이다.

\[L_{cos+xent}(x, y) = 1 - <\psi(f_{\theta}(x)), \varphi_{sem}(y)> - \lambda <\varphi_{onehot}(y), log(g_{\theta}(\psi(f_{\theta}(x))))>\]

이로써 categorical cross-entropy 보다 좋은 classification accuracy 성능을 기록하였다. 하지만 이 성능향상은 knowledge를 추가해서 라기보다 cosine loss를 사용해서 일어낸 결과이다.

Experiments

Datasets

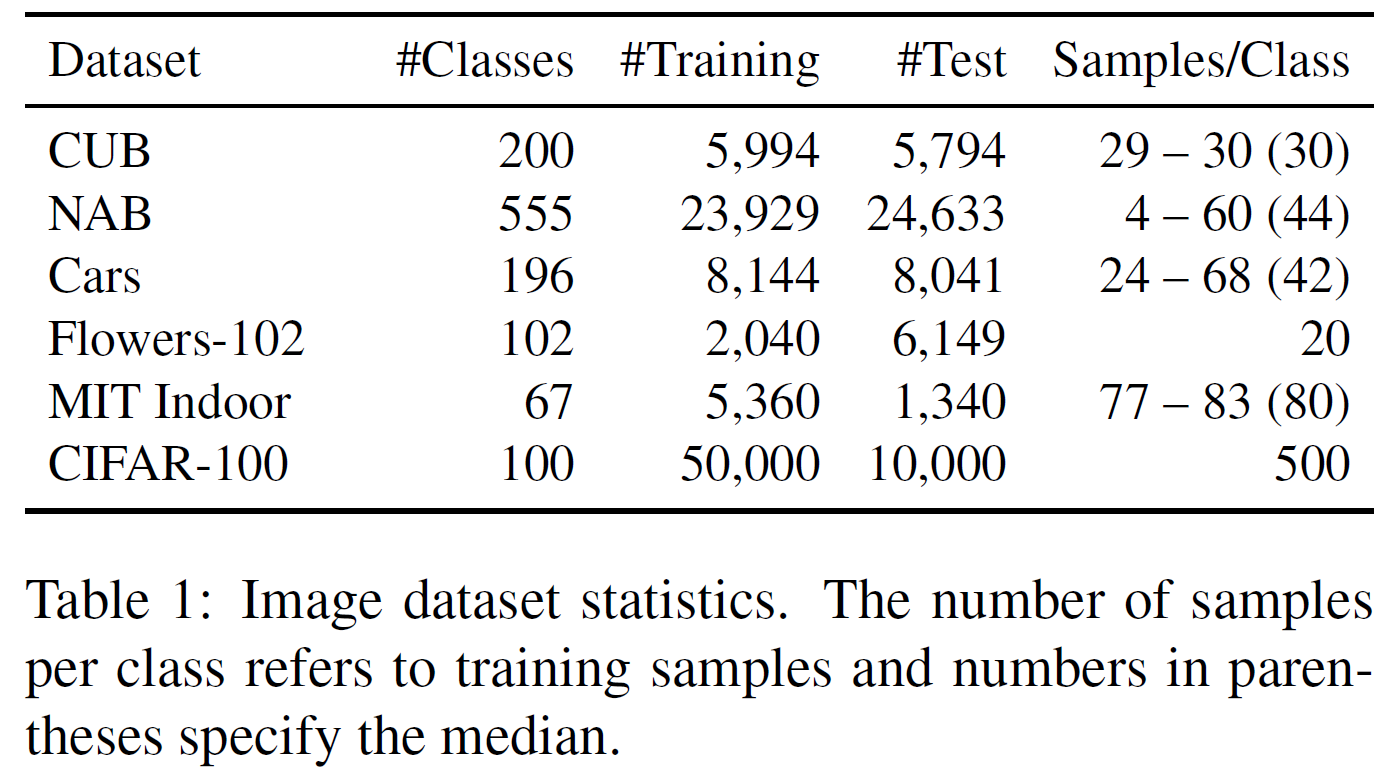
이미지 datasets(CUB, NAB, Cars, Flowers-102, MIT 67 Indoor Scenes, CIFAR-100) 뿐 아니라 text datasets(AG News)을 사용하였다. 각 데이터셋 마다의 세팅은 페이퍼에 잘 나와있다.

Performance Comparison

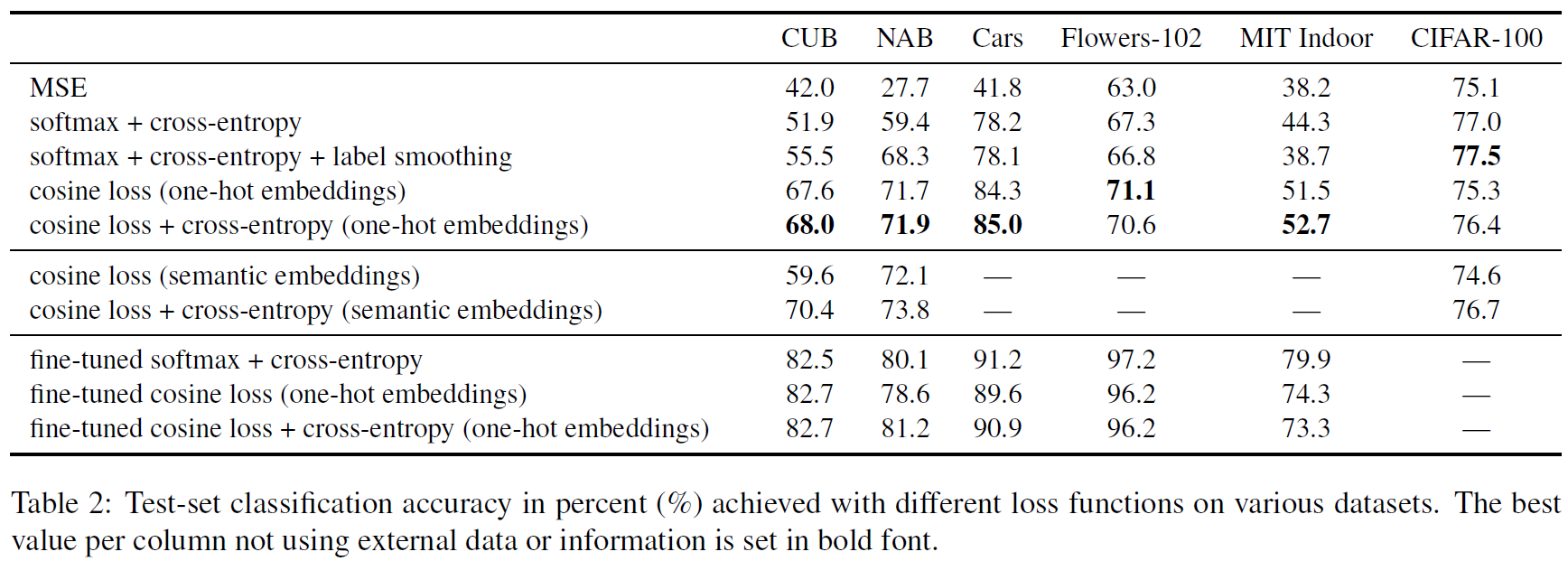
위 표를 보면 MSE, cross-entropy, cosine loss(one-hot embeddings or semantic embeddings), cosine loss + cross-entropy 등 여러가지 loss를 적용 했을 때의 accuracy를 측정하였다.

small dataset인 경우 cross-entropy를 사용했을 때 보다 cosine loss를 사용 했을 때 더 좋은 성능을 얻었다. 하지만 large dataset인 CIFAR-100의 경우 cross-entropy를 사용 했을 때 성능이 더 높은 것을 알 수 있다.

저자는 논문에서 fine-tuning로 학습한 성능과 차이가 줄어들 수 있을 것이라 얘기했다. 차이를 많이 줄인 것은 분명하지만, fine-tuning을 따라잡을 방법은 없을까..?

Effect of Semantic Information

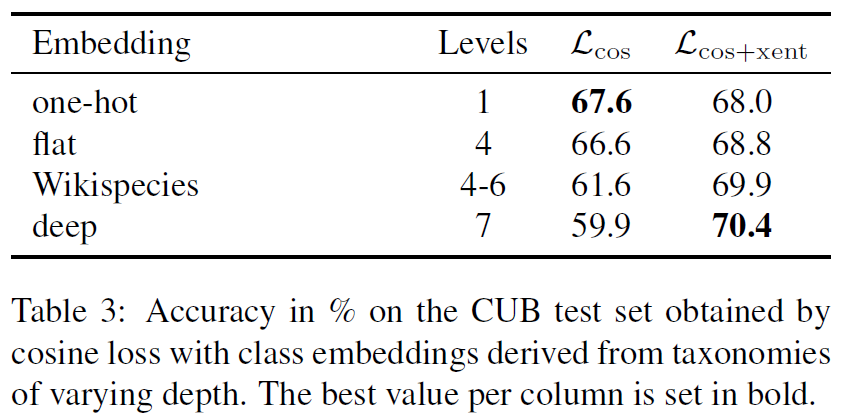
위 표를 보면 semantic information을 사용 했을 때 일반적인 cosine loss에 비해 약간의 성능 상승이 있었다.

위 표는 여러 embedding을 사용했을 떄의 성능을 보여준다. 계층 구조가 깊어질 수록 \(L_{cos+xent}\)의 성능이 상승하는 것을 확인 할 수 있다. semantic embedding은 유사한 클래스를 가까운 공간에 위치 시킨다 반면 다른 클래스는 멀리 떨어진 공간에 위치 시킨다. 따라서 cosine 유사도를 사용했을 때, 아예 다른(dissimilar) class의 고려를 덜하게 만들 수 있다.

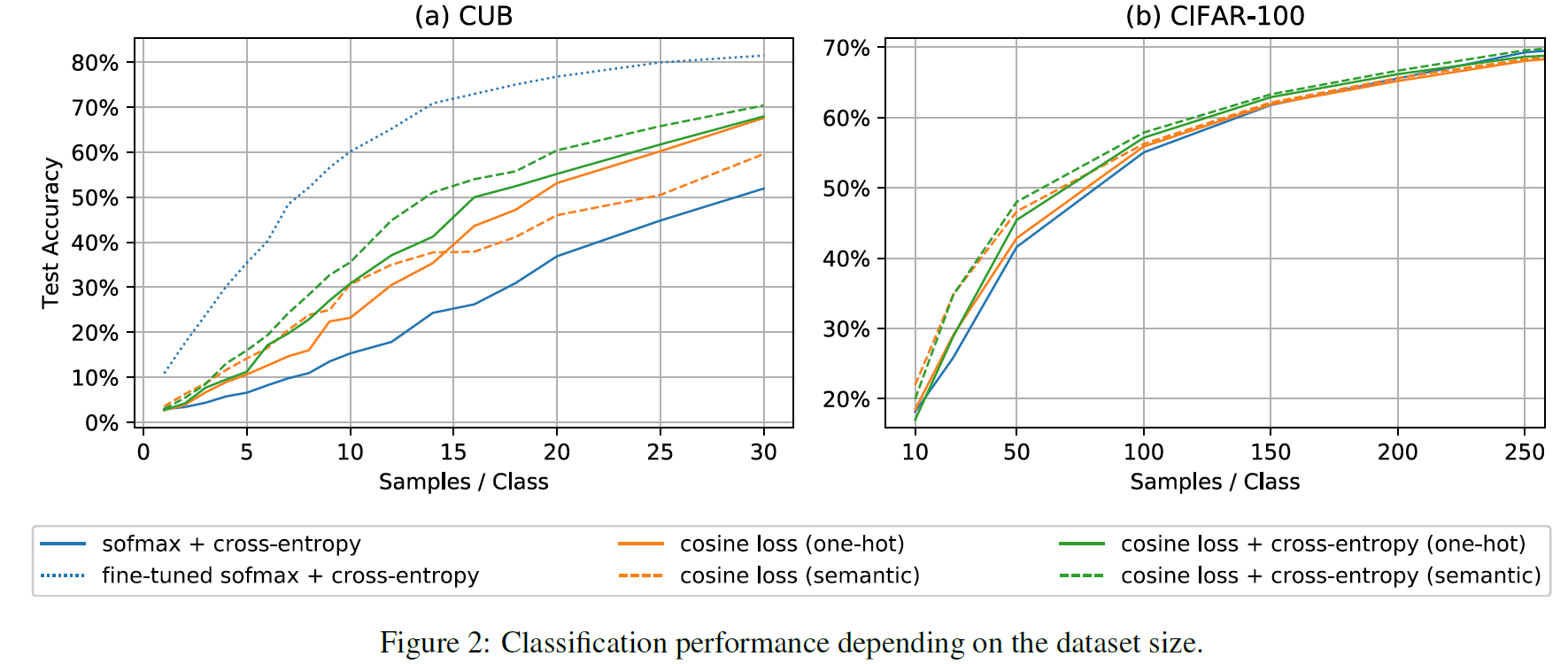
Effect of Dataset Size

위 figure을 보면 cosine loss는 일반적인 cross-entropy 보다 더 나은 성능을 보이며, 샘플을 추가할 때 더 빨리 개선된다. 또한 semantic information이 있을 때 가장 좋은 성능 개선이 이루어지는 것을 알 수 있다.

fine-tuned 모델은 이미 많은 데이터셋(ImageNet)을 사용하였기 때문에 가장 좋은 성능을 냈지만, Introduction에서 언급한 두 가지 문제가 있다. 따라서 본 논문의 cosine loss를 사용하는 것이 중요하다고 한다.

Review

비록 pre-trained model을 사용한 성능에는 미치지 않았지만, 단순히 loss를 바꿈으로써 기존 cross-entropy loss에 비해 높은 성능향상이 있었다는 점이 매우 흥미로웠다.

Reference

• Semantic Embedding