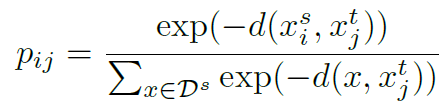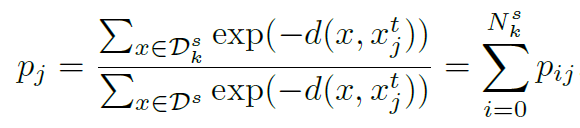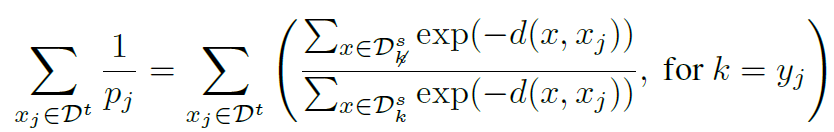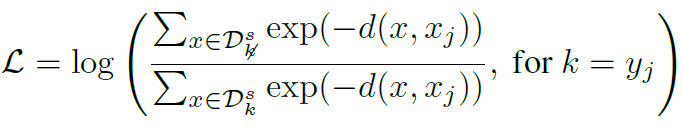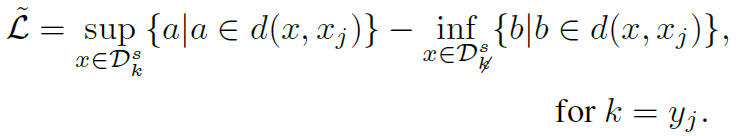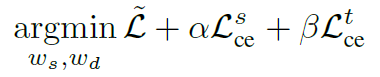CVPR 2019 에서 발표된 논문이다. (Arxiv

Code)

Domain Adaptation

Domain Adaptation 충분한 데이터가 없을 때에도 준수한 성능을 내기 위한 연구이다. Domain Adaptation 연구는 backpropagation 에 GRL(Gradient Reversal Layer)을 추가한 DANN, Discriminator를 이용한 ADDA, CycleGAN과 비슷한 방식으로 픽셀 레벨의 Domain Adaptation을 진행한 CyCADA, 두 도메인 사이의 거리를 고려한 DLOW 등 여러 방법으로 꾸준히 연구되어 왔다. Domain Adaptation은 간단히 얘기를 한다면 S(source) 도메인 데이터를 이용하여, T(target) 도메인에서 높은 성능을 내는 모델을 만드는 연구이다.

Introduction

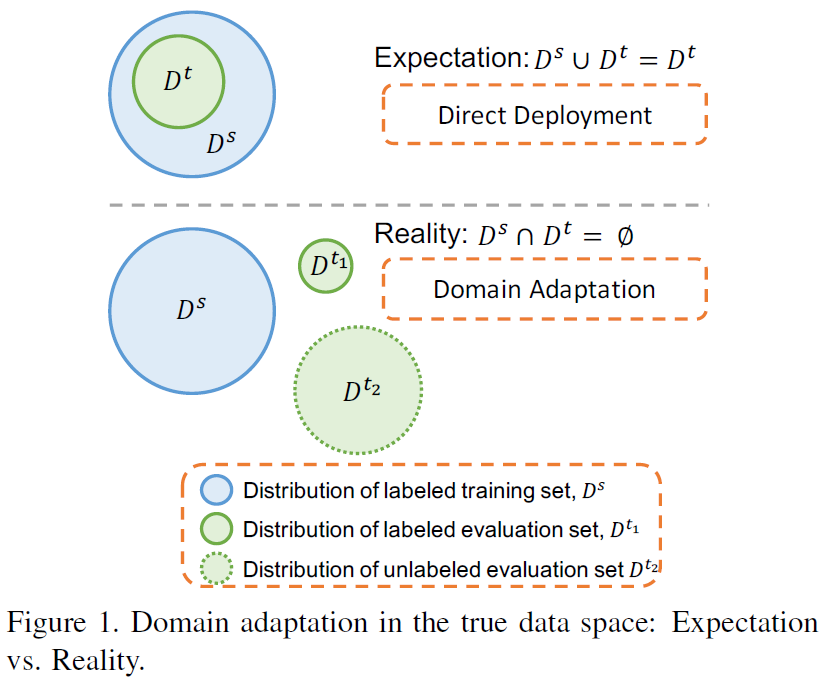
위 figure 상단 처럼 dataset \(D^T\) 이 \(D^S\) 안에 속한다면, 매우 운이 좋은 경우이다. 대개의 경우 하단과 같이 각 dataset의 distribution이 겹치지 않으며, 이로 인해 좋은 성능을 내기 어렵다. 이는 domain-shift 때문에 일어나는 현상이며, \(D^S\)으로 학습된 모델은 의미가 없어진다. Domain Adaptation은 위에 설명하듯이 다른 도메인의 성능을 높이는 일이며, 두 도메인 모두에서 동일한 성능을 갖게 된 경우를 Domain Generalization이라고 한다.

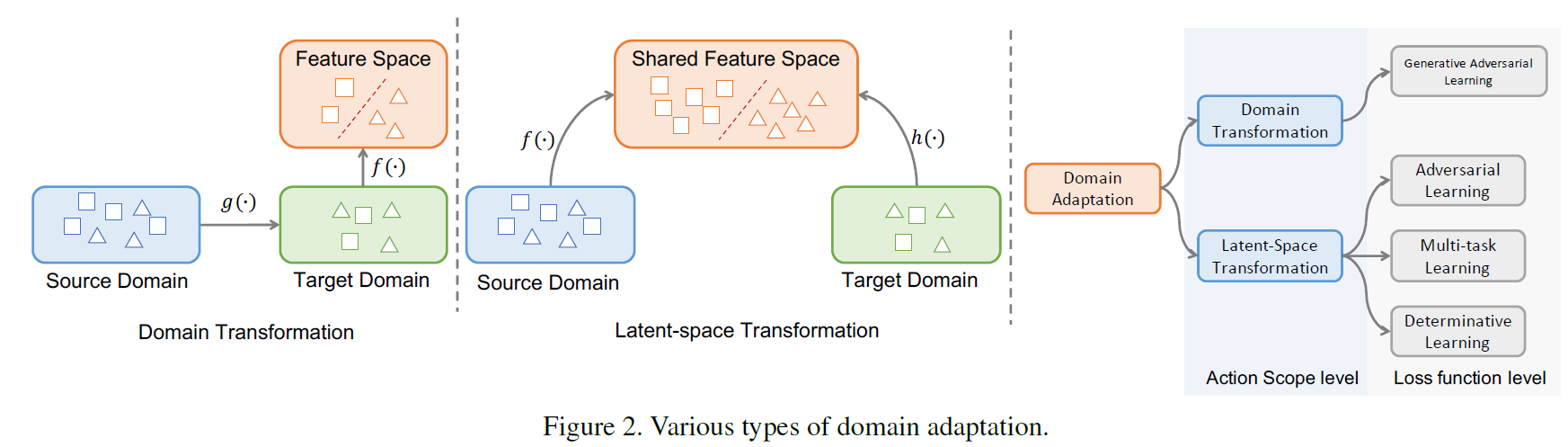
Domain Adaptation 에는 두가지 방법이 있다.

1. Domain Transformation
   • source 도메인으로 부터 학습된 모델을 사용하기 위해
   • target 도메인을 source 도메인으로 변환하는 방법
   • 주로 GAN based model이 사용된다.
2. Latent-Space Transformation:
   • source 도메인에서 추출한 feature와 target 도메인에서 추출한 feature을 동일한 latent space로 임베딩 시키는 방법

본 논문에서 소개하는 d-SNE은 두번째 방법을 이용한다. 여러 기법과 모델을 사용하였고, 자세한 내용은 바로 밑에서 다루겠다.

d-SNE

이 논문은 수식 쓰기가 너무 귀찮아서.. 이미지 파일로 대체…

\[d(x_{i}^s, x_{j}^t) = ||\Phi_{D^S}(x_{i}^s) - \Phi_{D^T}(x_{j}^t)||_{2}^2\]

위 수식은 latent-space에서 source domain (i번째 sample)과 target domain (j번째 sample)의 L2 distance를 뜻한다. 이때 \(\Phi_{D^s}\)는 source domain 데이터를 latent-space로 임베딩 시키는 neural networks이며, \(\Phi_{D^t}\) 또한 마찬가지이다.

위 수식은 j번째 target domain \(x_{j}^t\)와 source domain의 모든 데이터(\(x \in D^s\))의 거리 중 i번째 sample (\(x_{i}^s\))과의 거리 확률을 구하는 식이다. 거리가 가까울 수록 더 큰 값을 주기 위해 음수를 붙여 사용하였으며, softmax 함수를 이용하였다. 만약 \(x_{j}^t\)와 \(x_{i}^s\)가 같은 label을 가졌을때(\(y_{j}^t\) = \(y_{i}^s\)), \(p_{ij}\)가 크면 좋은 latent-space를 구축한 것이다.

\(x_{j}^t\)를 정확하게 예측할 확률 \(p_j\)는 위 식과 같다. 위 식에서 \(y_{j}^t = k\) 일때, \(y^s = k\) 인 \(x^s\)의 집합을 \(D_{k}^s\)로 두었다. 또한 \(D_{k}^s\)의 개수를 \(N_{k}^s\)으로 두었다. 여기서 중요한 점은 target sample(\(x_{j}^t, y_{j}^t=k\))이 주어졌을 때, \(D^s\)은 \(D_{k}^s\) 와 \(D_{\cancel{k}}^s\)로 나눠진다.

그래서 분모를 두개의 합으로 바꾸면 위 같은 식이 만들어진다. \(x_{j}^t\)를 정확히 예측하기 위해서는 \(p_j\)가 커져야 하기 때문에, 역수를 취해서 object function으로 사용할 수 있다. 이때 log를 씌어서 log-lieklihood를 줄이는 방향으로 학습이 이루어진다.

하지만 이 likelihood loss는 scaling issue가 생길 수 있고, adverse effect를 일으킬 수 있다고 한다. 이에 본 논문에서는 likelihood를 modified-Hausdorffian distnace를 사용해서 relax 시켰다. 단순히 같은 class를 갖고 있는 sample 중 가장 긴 거리를 줄이고, 다른 class를 갖고 있는 sample 중 가장 가까운 거리를 최대화 시키는 방향으로 Loss를 설계하였다. 위 식에서 sup는 supremum, inf는 infimum을 뜻한다.

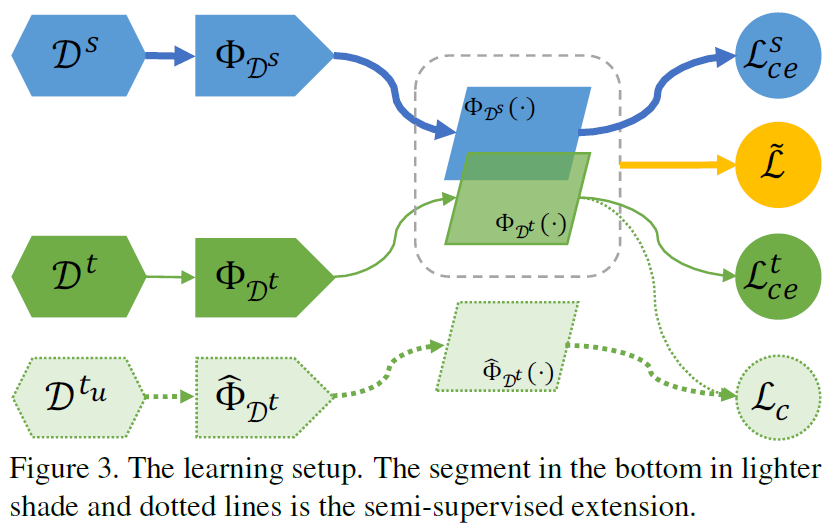
마지막으로 각 모델(\(\Phi_{D^s}\), \(\Phi_{D^t}\))은 cross-entropy loss로도 학습이 된다. 따라서 learning formulation은 위와 같다. 각각 독립적으로 weight update를 하도록 하며, 위 figure 3에서 잘 나타내진다.

마지막으로 unlabeled data를 이용하여 성능을 boost 시키기 위해, semi-supervised learning을 진행하였다. Mean-Teacher 모델과 유사하게 학습을 시켰다고한다. Mean-Teacher 모델은 다음과 같다.

1. input image를 student 그리고 teacher 모델을 통해 각각 prediction을 얻은다.
   • student, teacher 모델에는 noise를 추가한다.
2. 이때 두 prediction의 consistency cost를 이용하여 student model을 학습시킨다.
3. label과 classification cost를 이용하여 student model을 학습시킨다.
4. 학습된 student model weights를 이용하여 teacher model weights를 업데이트 한다.
   • exponential moving average 이용
5. unlabeled data인 경우 3의 단계는 제외한다.

Experiments

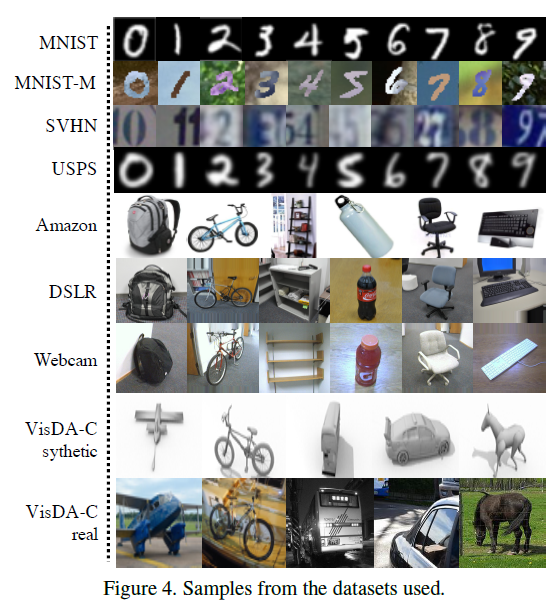
세가지 종류의 데이터셋을 이용하여 실험을 하였다.

1. digits datasets
   • MNIST
   • MNIST-M
   • USPS
   • SVHN
2. office datasets
   • Office-31A (in Amazon)
   • Office-31D (using DSLR)
   • Office-31W (using web camera)
3. VisDA-C datasets
   • VisDA-C sythetic
   • VisDA-C real

위 figure은 데이터의 분포를 시각화 한 것이다. domain adaptation을 적용한(bottom) 실험이 데이터 분포를 잘 나누는 것을 알 수 있다.

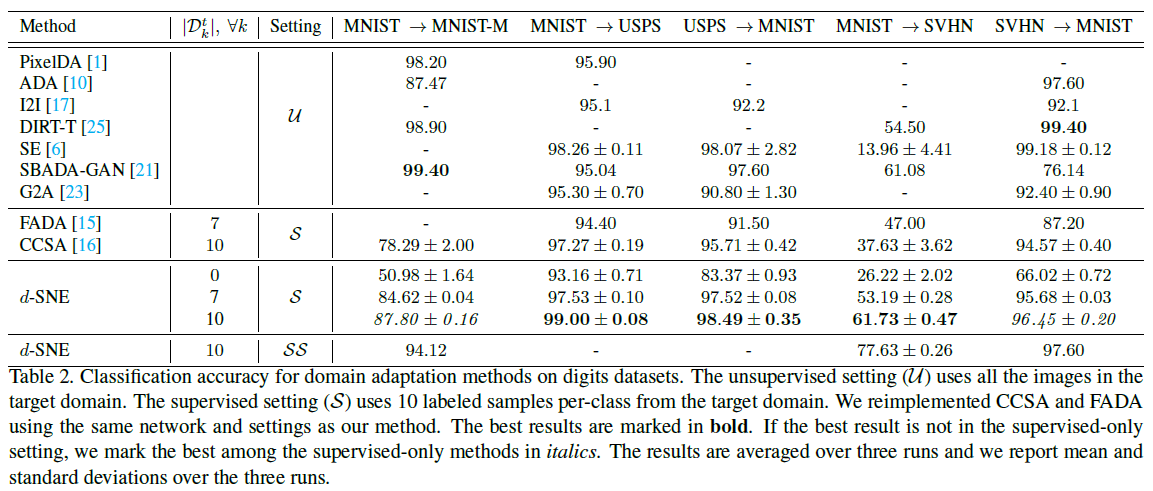
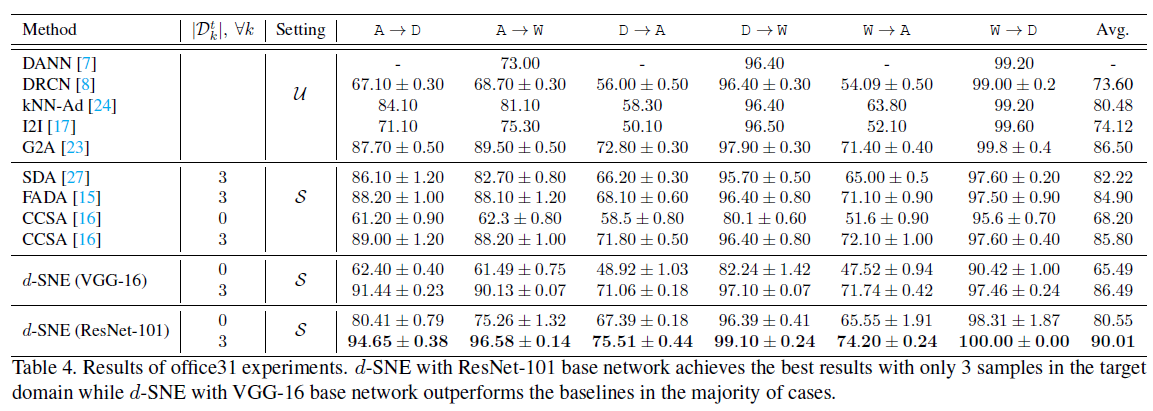
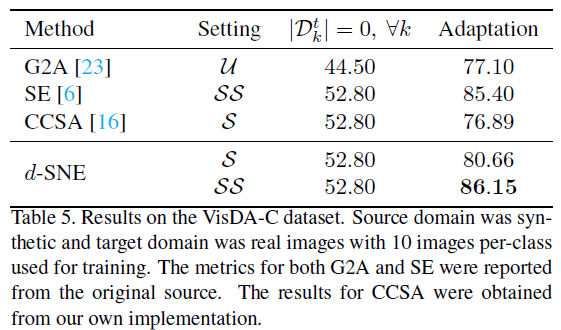
위는 각 실험들의 결과이다. 타 모델보다 d-SNE 모델이 대체로 좋은 성능을 내는 것을 확인할 수 있다. 표의 Setting에서 U가 뜻하는 것은 모든 target domain data를 사용해서 unsupervised learning을 진행한 것이고, S는 각 클래스당 표의 \(D_{k}^t\)개수 만큼 labeled target domain data를 이용하여 학습한 것이다.

Review

Training 혹은 inference에 관한 자세한 설명이 없어서 아쉬웠지만, 얼추 추측이 가능한 레벨이기 때문에 이해할 수 있었던 것 같다. 이 paper를 읽으면서 domain adaptation에 관한 잘못된 지식을 고친 것 같다.

Reference

• Mean-Teacher